Горизонтко бурч менен ыргытылган
нерсенин кыймылы

 

 

Жабдуулар:    

                    -    атуучу түзүлүш;

-         пластик топтору;

-         метрдик тасма;

-         сызгыч;

-         көчүрмө кагазы (копирка);

-         ак кагаз;

-         миллиметрдик кагаз

 

 

Максат:  Горизонталдык багытта ыргытылган нерсенин учуу алыстыгын аныктоо;

          Горизонтко бурч  менен ыргытылган нерсенин учуу алыстыгын аныктоо;

          Нерсенин учуу алыстыгы менен атуу бурчунун ортосундагы байланышты табуу.

 

 

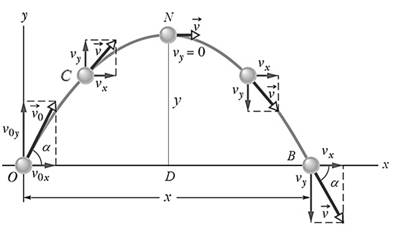
5.1-сүрөт

Ийри сызыктуу кыймылдардын ичинен горизонтко бурч менен ыргытылган нерселердин кыймылдарын өз алдынча бөлүп кароо ылайык. Себеби, мындай мүнөздөгү кыймылдарга артиллериялык куралдардан атылып чыккан снаряддар, самолеттон ташталган бомба жана жүк, биз ыргыткан нерселер ж.у.с. көп мисалдарды келтирүүгө болот.

Абанын каршылыгын эске албаганда, мындай кыймылдардын негизги теңдемесин төмөнкүчө аныктайбыз.

Нерсе, убакыттын  моментинде, координат башталышынан,  ылдамдыкта горизонтко ( огуна) карата  бурчу менен ыргытылсын дейли (5.1-сүрөт). Анда  баштапкы ылдамдыгы  огуна карата  (горизонталдык) жана  огуна карата  (вертикалдык) түзүүчүлөрүнө ээ болот:

 

,

.

Кандайдыр  убактысы өткөндөн кийин, нерсе  чекитине жетип,  ылдамдыгына ээ болсун. Бул ылдамдыкты да горизонталдык жана вертикалдык түзүүчүлөргө ажыратып, аларды аныктайлы.

Учуп бараткан нерсеге,  горизонталдык багытта  эч кандай күч таасир этпегендиктен (абанын каршылыгын эске албаганда), ылдамдыктын горизонталдык түзүүчүсү бүткүл жолдо турактуу сакталат, б.а. . Ал эми вертикалдык түзүүчүсү, Жердин гравитациялык талаасынын (күчүнүн) таасиринен, нерсенин жогору көтөрүлүшү менен кичирейип, ал эми төмөн түшүшү менен чоңоюп отурат. Бул өзгөрүү боюнча болот. Ошондуктан, жогорудагы системаны  убакыт моменти үчүн төмөнкүчө жазабыз:

 

Мында  - эркин түшүүнүн ылдамдануусу.

Биз карап жаткан убакыт ичиндеги нерсенин горизонталдык жана вертикалдык багыттар боюнча өткөн жолдору  жана , б.а.  чекитинин ,  координаталары төмөнкүчө болору шексиз:

Бул эки теңдемеден нерсенин кыймылынын траекториясын аныктоого болот. Ал үчүн убакытты жоготобуз. (5.2) теңдемеден

 

маанисин (5.3)  теңдемеге коебуз:

 жана  турактуу болгондуктан, жогорку теңдеме

 

теңдемесинин түрүнө келет. Бул теңдеме параболанын теңдемеси. Ошентип, горизонтко бурч боюнча багытталган нерсенин кыймылы (траекториясы), абанын каршылыгын эсепке албаганда, парабола боюнча болот.

Жогорудагы (5.1), (5.2), (5.3) (5.4) теңдемелерди пайдаланып, горизонтко бурч менен багытталган нерсенин кыймылынын дагы бир катар мүнөздөмөлөрүн аныктоого болот.

Нерсенин учуу алыстыгынын жана көтөрүлүү бийиктигинин бурчтан көз карандылыгы. Нерсенин көтөрүлгөн эң чоң бийиктиги, б.а. параболанын чокусу жана анын учуу алыстыгы  менен  бурчунан кандай көз каранды экендигин иликтеп көрөлү.

Параболанын эң бийик чекитинде, б.а. параболанын чокусунда . Эгерде  бул чокуга чейин нерсенин көтөрүлүүсүнө кеткен убакыт деп эсептесек, анда (5.1) системасынын экинчи теңдемесинен

 

Убакыттын ушул маанисин (5.3) теңдемесине коюп,

 

алабыз. Турактуу  үчүн көтөрүлүү бийиктиги  дан гана көз каранды. Бурч  болгондо, көтөрүлүү эң бийик болот:

 

Демек, бул учур үчүн көтөрүлүү  дон гана көз каранды. Берилген бурч үчүн, баштапкы ылдамдыктын чоңоюшу менен нерсенин көтөрүлүү бийиктиги да чоңоет.

Горизонтко бурч боюнча багытталган нерсенин учуу алыстыгын билүү да чоң мааниге ээ. Нерсенин учуу алыстыгы – бул нерсенин чыккан чекитинин горизонталдык проекциясынан баштап анын түшүү чекитине чейинки аралык. Ал жогорудагы (5.2) формуласы менен аныкталарын эскерттик. Мында   - горизонтко карата бурч, б.а.  баштапкы ылдамдык вектору менен горизонт сызыгынын ортосундагы бурч экендигин тактай кетели (5.1-сүрөт).

Эгерде нерсенин атылуу бийиктиги менен түшүү бийиктиги бирдей деңгээлде, б.а.  жана  чекиттери бир тегиздикте жатса, горизонталдык багыт боюнча  аралыгын өтүү үчүн канча убакыт кетсе,  аралыгын өтүү үчүн кеткен убакыт да ошондой эле болот. Анда жалпы учуу убактысы нерсенин максималдуу көтөрүлүү чекитине жетүүгө кеткен убакыттын эки эселенгенине барабар болот:

 

 

Ушул себептен  аралыгын табуу үчүн (5.2) теңдемесине (5.8) теңдемесин коюп, төмөнкүгө ээ болобуз:

 

 

Бирдей  үчүн  болгондо учуу алыстыгы эң чоң б.а.

болот.

Баштапкы ылдамдыкты аныктоо. Горизонтко карата кандайдыр бир бурч менен ыргытылган нерсенин учуу алыстыгын аныктоо үчүн, адегенде, нерсенин баштапкы (ыргытылган учурдагы)  ылдамдыгын  табуу керек. Ал үчүн нерсени горизонталдык багытта атып, атуучу түзүлүштүн бийиктигин, б.а. баштапкы бийиктикти жана нерсенин учуу алыстыгын өлчөө керек.

Нерсе кандайдыр бир бийиктиктен горизонталдык багытта ыргытылганда, б.а. болгон учурда (5.3) формуласы төмөндөгүдөй түргө келет:

 

Мында,  нерсенин баштапкы учуп чыгуу бийиктиги го барабар деп алабыз. Баштапкы бийиктикти өлчөө менен, (5.11) теңдемесинен нерсенин учуу убактысын аныктоого болот:

 

(5.2) теңдемесин  учуру үчүн жазсак

болот. Анда баштапкы ылдамдык төмөнкү формула менен аныкталып калат:

 

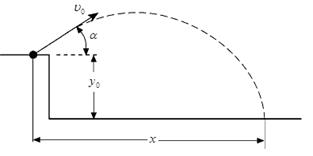
Бийиктиктен бурч менен атылган топтун учуу алыстыгын аныктоо. Эгерде нерсе белгилүү бийиктиктен горизонтко кандайдыр бир бурч менен атылса (5.2-сүрөт), анда анын кыймылын, жогоруда каралган эки учур: жерден горизонтко белгилүү бир бурч менен жана белгилүү бийиктиктен горизонталдык багытта ыргытылган нерселердин кыймылдарынын комбинациясы катары карап, аларга тиешелүү болгон (5.1)-(5.10) жана (5.11)-(5.14) теңдемелери менен мүнөздөөгө болот. Мында нерсе параболанын чокусунда ээ болгон ылдамдыгы,  баштапкы ылдамдыктын  горизонталдык түзүүчүсүнө барабар экендигин белгилей кетүү зарыл.

 

5.2-сүрөт